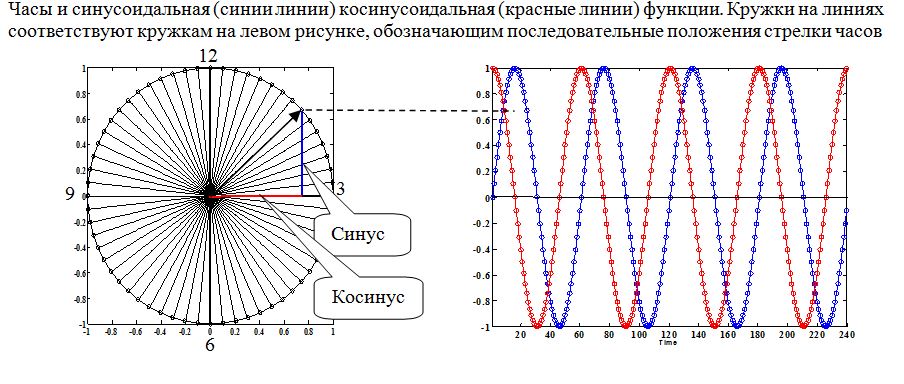
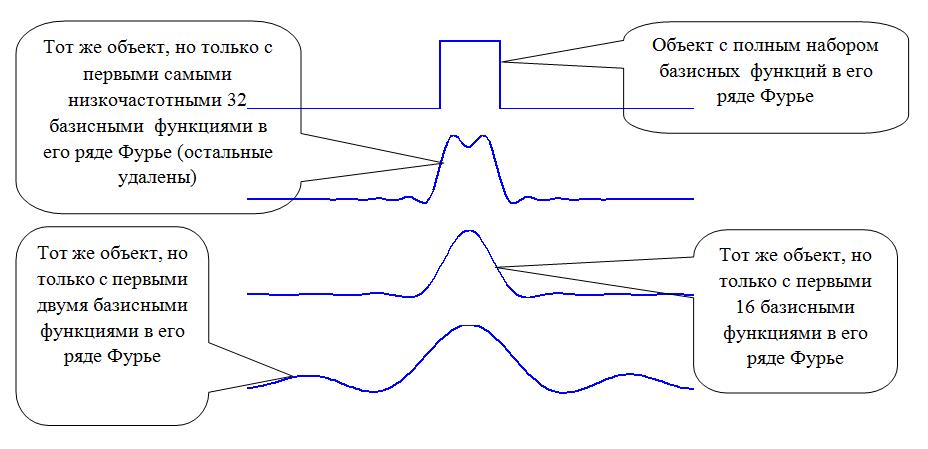
Что такое ряды Фурье,
или можно ли быть сразу здесь и везде, сейчас и всегда?

|
|

6
|
|
Для любознательных молодых людей любого возраста, которые любят смотреть интернет телевидение и пользоваться цифровыми фото и видео камерами, а при случае и непрочь задуматься о том, как устроена природа |
Что такое ряды Фурье,
или можно ли быть сразу здесь и везде, сейчас и всегда?


|
|


6
|
|
|